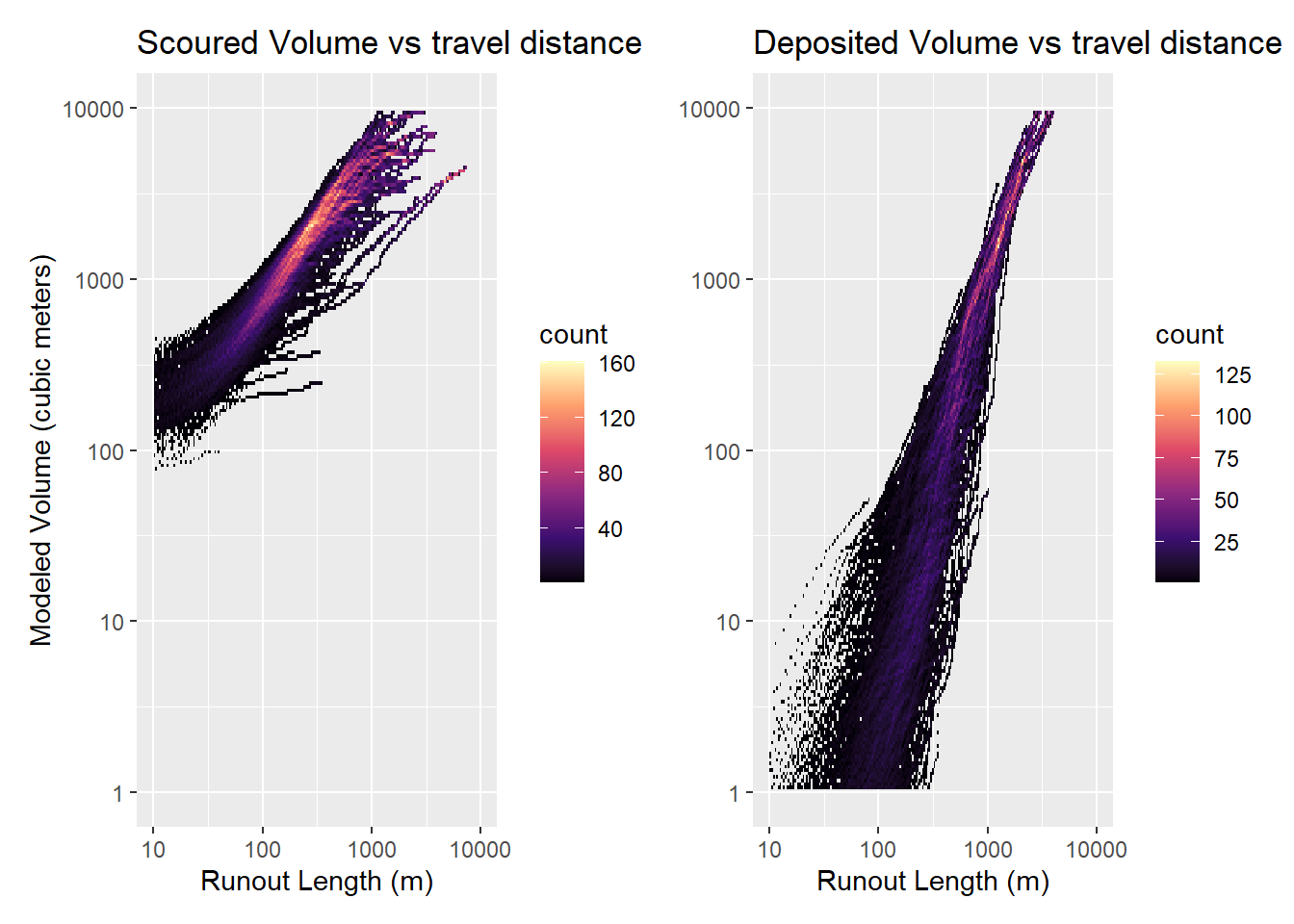
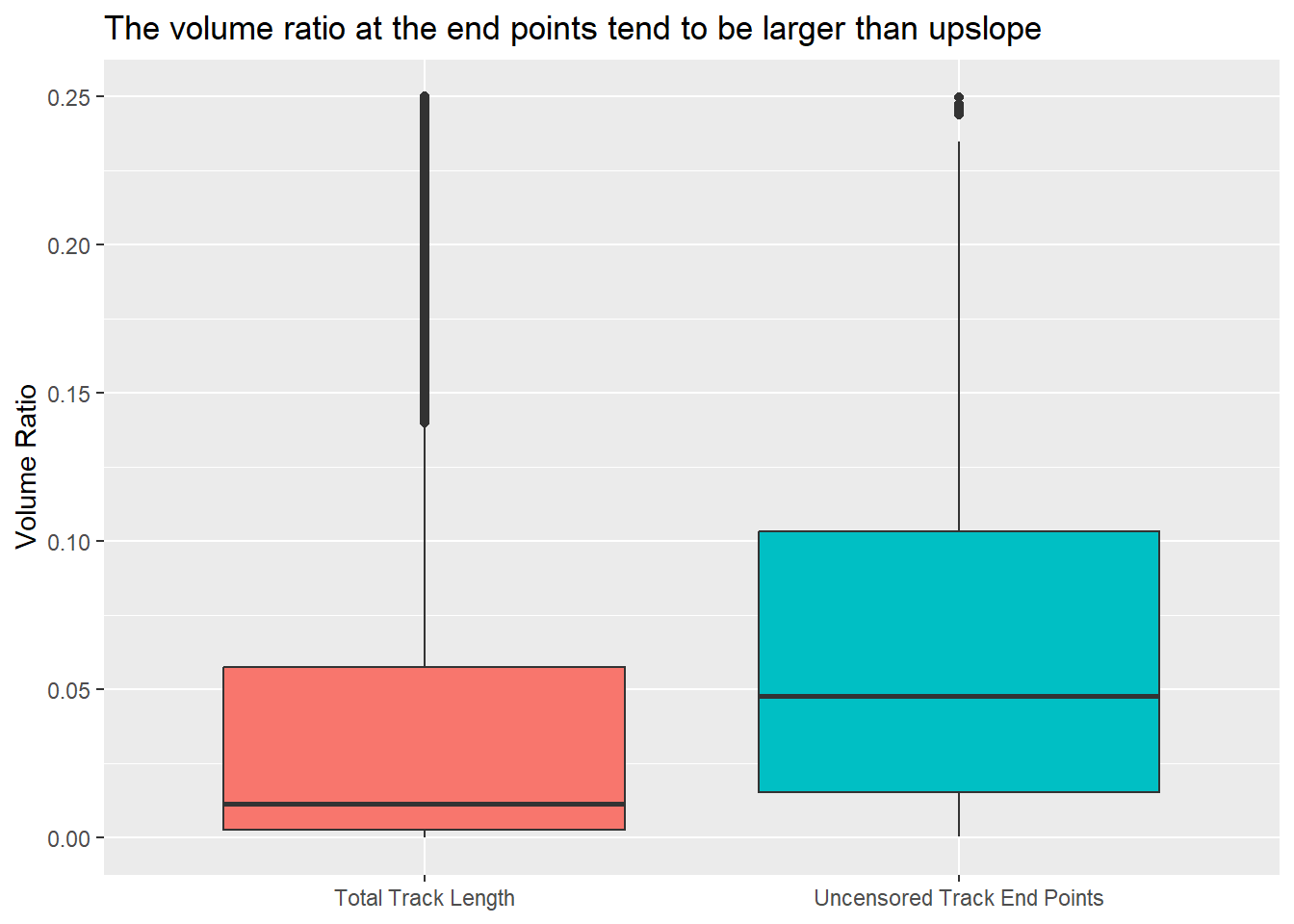
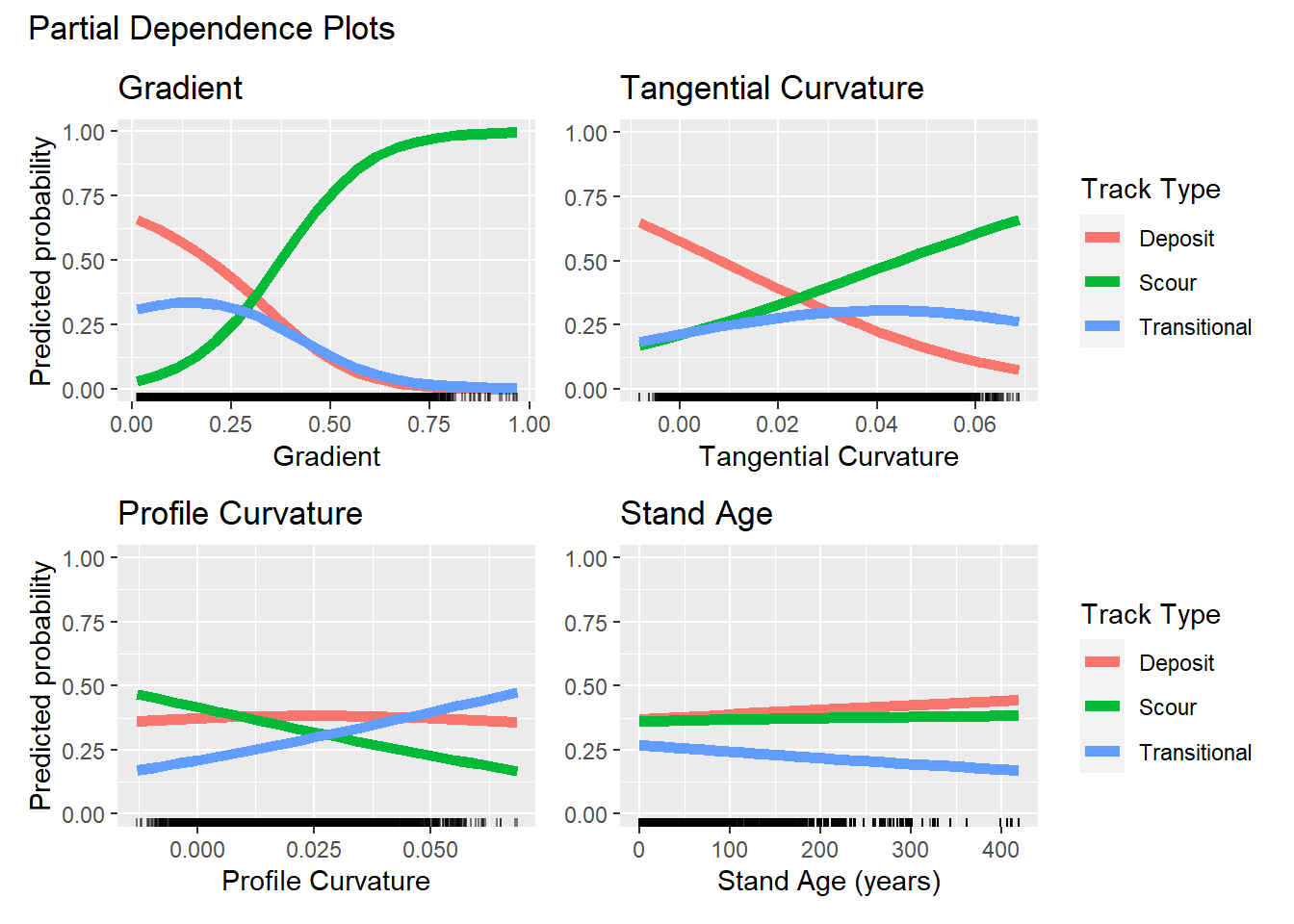
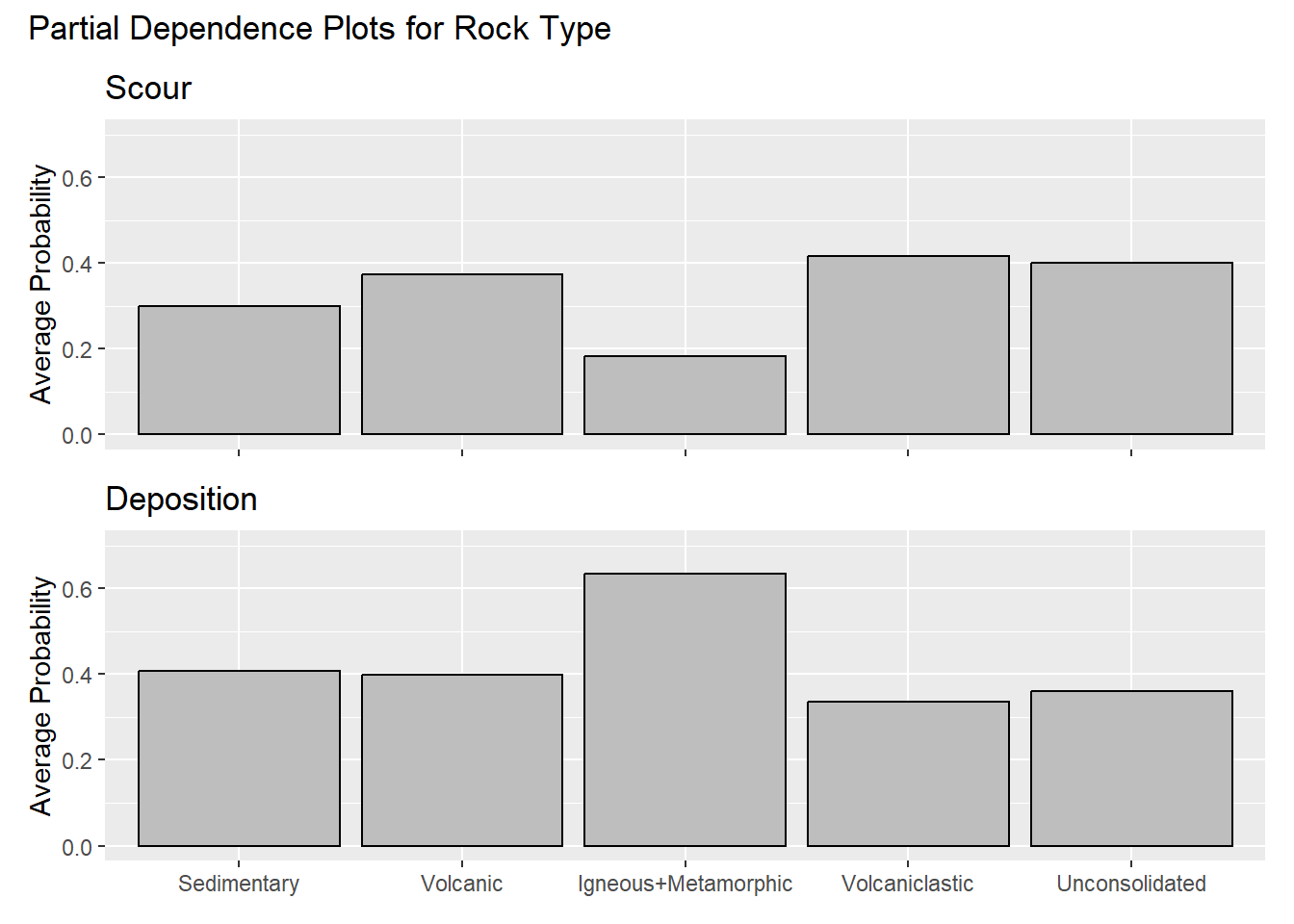
Alarid-Escudero, Fernando, Eline M. Krijkamp, Petros Pechlivanoglou, Hawre Jalal, Szu-Yu Zoe Kao, Alan Yang, and Eva A. Enns. 2019.
“A Need for Change! A Coding Framework for Improving Transparency in Decision Modeling.” PharmacoEconomics 37 (11): 1329–39.
https://doi.org/10.1007/s40273-019-00837-x.
Barnes, Richard, Clarence Lehman, and David Mulla. 2014.
“Priority-Flood: An Optimal Depression-Filling and Watershed-Labeling Algorithm for Digital Elevation Models.” Computers & Geosciences 62 (January): 117–27.
https://doi.org/10.1016/j.cageo.2013.04.024.
Benda, Lee. 1990.
“The Influence of Debris Flows on Channels and Valley Floors in the Oregon Coast Range, U.S.A.” Earth Surface Processes and Landforms 15 (5): 457–66.
https://doi.org/10.1002/esp.3290150508.
Benda, Lee E., and Terrance W. Cundy. 1990.
“Predicting Deposition of Debris Flows in Mountain Channels.” Canadian Geotechnical Journal 27 (4): 409–17.
https://doi.org/10.1139/t90-057.
Bernard, Thomas G., Dimitri Lague, and Philippe Steer. 2021.
“Beyond 2D Landslide Inventories and Their Rollover: Synoptic 3D Inventories and Volume from Repeat Lidar Data.” Earth Surface Dynamics 9 (4): 1013–44.
https://doi.org/10.5194/esurf-9-1013-2021.
Bettella, Francesco, Tamara Michelini, Vincenzo D’Agostino, and Gian Battista Bischetti. 2018.
“The Ability of Tree Stems to Intercept Debris Flows in Forested Fan Areas: A Laboratory Modelling Study.” Journal of Agricultural Engineering 49 (1): 42–51.
https://doi.org/10.4081/jae.2018.712.
Boettinger, Janis L., David W. Howell, Amanda C. Moore, Alfred E. Hartemink, and Suzann Kienast-Brown, eds. 2010.
Digital Soil Mapping. Springer Netherlands.
https://doi.org/10.1007/978-90-481-8863-5.
Booth, Adam M., Christian Sifford, Bryce Vascik, Cora Siebert, and Brian Buma. 2020.
“Large Wood Inhibits Debris Flow Runout in Forested Southeast Alaska.” Earth Surface Processes and Landforms 45 (7): 1555–68.
https://doi.org/10.1002/esp.4830.
Burnett, K. M., and D. J. Miller. 2007. “Streamside Policies for Headwater Channels: An Example Considering Debris Flows in the Oregon Coastal Province.” Forest Science 53 (2): 239–53.
Burns, W. J., J. J. Franczyk, and N. C. Calhoon. 2022.
“Protocol for Channelized Debris Flow Susceptibility Mapping.” Special Paper 53. Oregon Department of Geology; Mineral Resources.
https://www.oregongeology.org/pubs/sp/SP-53/p-SP-53.htm.
Clarke, Sharon E., Kelly M. Burnett, and Daniel J. Miller. 2008.
“Modeling Streams and Hydrogeomorphic Attributes in Oregon From Digital and Field Data1.” JAWRA Journal of the American Water Resources Association 44 (2): 459–77.
https://doi.org/10.1111/j.1752-1688.2008.00175.x.
Coe, Jeffrey A. 2011.
“Assessment of topographic and drainage network controls on debris-flow travel distance along the west coast of the United States.” Italian Journal of Engineering Geology and Environment, no. 201103 (June): 199–209.
https://doi.org/10.4408/IJEGE.2011-03.B-024.
Coho, C., and S. J. Burges. 1993.
“Dam-Break Floods in Low Order Mountain Channels of the Pacific Northwest.” TFW-SH9-93-001. Department of Civil Engineering, University of Washington.
https://www.dnr.wa.gov/publications/fp_tfw_sh9_93_001.pdf.
DeLong, S. B., M. N. Hammer, Z. T. Engle, E. M. Richard, A. J. Breckenridge, K. B. Gran, C. E. Jennings, and A. Jalobeanu. 2022.
“Regional-Scale Landscape Response to an Extreme Precipitation Event From Repeat Lidar and Object-Based Image Analysis.” Earth and Space Science 9 (12).
https://doi.org/10.1029/2022ea002420.
Dietrich, W. E., and T. Dunne. 1978. “Sediment Budget for a Small Catchment in Mountainous Terrain.” Zietshrift Für Geomorphologie Suppl. Bd. 29: 191–206.
Dietrich, W. E., T. Dunne, N. F. Humphrey, and L. M. Reid. 1982. “Construction of Sediment Budgets for Drainage Basins.” In Sediment Budgets and Routing in Forested Drainage Basins, General Technical Report PNW-141, 5–23. US Department of Agriculture, Forest Service.
Emmert-Streib, Frank, and Matthias Dehmer. 2019.
“Introduction to Survival Analysis in Practice.” Machine Learning and Knowledge Extraction 1 (3): 1013–38.
https://doi.org/10.3390/make1030058.
Fannin, R J, and M P Wise. 2001.
“An Empirical-Statistical Model for Debris Flow Travel Distance.” Canadian Geotechnical Journal 38 (5): 982–94.
https://doi.org/10.1139/t01-030.
Fannin, R. J., and T. P. Rollerson. 1993.
“Debris Flows: Some Physical Characteristics and Behaviour.” Canadian Geotechnical Journal 30 (1): 71–81.
https://doi.org/10.1139/t93-007.
Griswold, J. P., and R. M. Iverson. 2008.
“Mobility Statistics and Automated Hazard Mapping for Debris Flows and Rock Avalanches.” USGS Scientific Investigations Report, no. 2007-5276.
http://pubs.usgs.gov/sir/2007/5276/.
Guthrie, R. H., A. Hockin, L. Colquhoun, T. Nagy, S. G. Evans, and C. Ayles. 2010.
“An Examination of Controls on Debris Flow Mobility: Evidence from Coastal British Columbia.” Geomorphology 114 (4): 601–13.
https://doi.org/10.1016/j.geomorph.2009.09.021.
Guthrie, Richard, and Andrew Befus. 2021.
“DebrisFlow Predictor: An Agent-Based Runout Program for Shallow Landslides.” Natural Hazards and Earth System Sciences 21 (3): 1029–49.
https://doi.org/10.5194/nhess-21-1029-2021.
Hofmeister, R. J., D. J. Miller, K. A. Mills, J. C. Hinkle, and A. C. Beier. 2002.
“Hazard Map of Potential Rapidly Moving Landslides in Western Oregon, Interpretive Map Series - 22.” Oregon Department of Geology; Mineral Industries.
https://www.oregongeology.org/pubs/ims/p-ims-022.htm.
Horton, P., M. Jaboyedoff, B. Rudaz, and M. Zimmermann. 2013.
“Flow-R, a Model for Susceptibility Mapping of Debris Flows and Other Gravitational Hazards at a Regional Scale.” Natural Hazards and Earth System Sciences 13 (4): 869–85.
https://doi.org/10.5194/nhess-13-869-2013.
Ishikawa, Yoshiharu, Sunao Kawakami, Chiyo Morimoto, and Kunio Mizuhara. 2003.
“Suppression of Debris Movement by Forests and Damage to Forests by Debris Deposition.” Journal of Forest Research 8 (1): 37–47.
https://doi.org/10.1007/s103100300004.
Iverson, Richard M., Steven P. Schilling, and James W. Vallance. 1998.
“Objective Delineation of Lahar-Inundation Hazard Zones.” Geological Society of America Bulletin 110 (8): 972–84.
https://doi.org/10.1130/0016-7606(1998)110<0972:odolih>2.3.co;2.
Jakob, Matthias, and Hamish Weatherly. 2007.
“Integrating Uncertainty: Canyon Creek Hyperconcentrated Flows of November 1989 and 1990.” Landslides 5 (1): 83–95.
https://doi.org/10.1007/s10346-007-0106-z.
Jenson, S. K., and J. O. Dominque. 1997.
“Extracting Topographic Structure from Digital Elevatiojn Data for Geographic Information System Analysis.” Photogrammetric Engineering and Remote Sensing 54 (11): 1593–1600.
https://www.asprs.org/wp-content/uploads/pers/1988journal/nov/1988_nov_1593-1600.pdf.
Johnson, A. C. 1991.
“Effects of Landslide-Dam-Break Floods on Channel Morphology.” Master’s thesis, University of Washington.
https://www.dnr.wa.gov/publications/fp_tfw_land_dam_brea_1991.pdf.
Kalbfleisch, John D., and Ross L. Prentice. 2002.
The Statistical Analysis of Failure Time Data. John Wiley & Sons, Inc.
https://doi.org/10.1002/9781118032985.
Keck, Jeffrey, Erkan Istanbulluoglu, and Erkan Istanbulluoglu. 2021.
“MASS WASTING RUNOUT: A SIMPLE MODEL FOR PREDICTING LANDSLIDE RUNOUT AND THE TOPOGRAPHIC EVOLUTION OF HEADWATER CHANNELS.” Geological Society of America Abstracts with Programs.
https://doi.org/10.1130/abs/2021am-368944.
Lancaster, Stephen T., Shannon K. Hayes, and Gordon E. Grant. 2003.
“Effects of Wood on Debris Flow Runout in Small Mountain Watersheds.” Water Resources Research 39 (6).
https://doi.org/10.1029/2001wr001227.
Marshall, Jill A., and Joshua J. Roering. 2014.
“Diagenetic Variation in the Oregon Coast Range: Implications for Rock Strength, Soil Production, Hillslope Form, and Landscape Evolution.” Journal of Geophysical Research: Earth Surface 119 (6): 1395–1417.
https://doi.org/10.1002/2013jf003004.
Marwick, Ben, Carl Boettiger, and Lincoln Mullen. 2018.
“Packaging Data Analytical Work Reproducibly Using R (and Friends).” The American Statistician 72 (1): 80–88.
https://doi.org/10.1080/00031305.2017.1375986.
May, C. L. 1998.
“Debris Flow Characteristics Associated with Forest Practices in the Central Oregon Coast Range.” Master’s thesis, Oregon State University.
https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/d217qr764.
May, Christine L. 2002.
“DEBRIS FLOWS THROUGH DIFFERENT FOREST AGE CLASSES IN THE CENTRAL OREGON COAST RANGE.” Journal of the American Water Resources Association 38 (4): 1097–1113.
https://doi.org/10.1111/j.1752-1688.2002.tb05549.x.
May, Christine L., and Robert E. Gresswell. 2003.
“Processes and Rates of Sediment and Wood Accumulation in Headwater Streams of the Oregon Coast Range, USA.” Earth Surface Processes and Landforms 28 (4): 409–24.
https://doi.org/10.1002/esp.450.
Michelini, Tamara, Francesco Bettella, and Vincenzo D’Agostino. 2017.
“Field Investigations of the Interaction Between Debris Flows and Forest Vegetation in Two Alpine Fans.” Geomorphology 279 (February): 150–64.
https://doi.org/10.1016/j.geomorph.2016.09.029.
Mikoš, Matjaž, and Nejc Bezak. 2021.
“Debris Flow Modelling Using RAMMS Model in the Alpine Environment with Focus on the Model Parameters and Main Characteristics.” Frontiers in Earth Science 8 (January).
https://doi.org/10.3389/feart.2020.605061.
Miller, D. J., L. Benda, J. DePasquale, and D. Albert. 2015.
“Creation of a Digital Flowline Network from IfSAR 5-m DEMs for the Matanuska-Susitna Basins: A Resource for Update of the National Hydrographic Dataset in Alaska.” The Nature Conservancy.
https://www.conservationgateway.org/ConservationByGeography/NorthAmerica/UnitedStates/alaska/scak/Documents/Miller_etal_MatSu_Elevation_Derived_Flow_Network_Report.pdf.
Miller, Daniel J., and Lee E. Benda. 2000.
Geological Society of America Bulletin 112 (12): 1814.
https://doi.org/10.1130/0016-7606(2000)112<1814:eopsso>2.0.co;2.
Miller, Daniel J., and Kelly M. Burnett. 2007.
“Effects of Forest Cover, Topography, and Sampling Extent on the Measured Density of Shallow, Translational Landslides.” Water Resources Research 43 (3).
https://doi.org/10.1029/2005wr004807.
———. 2008.
“A Probabilistic Model of Debris-Flow Delivery to Stream Channels, Demonstrated for the Coast Range of Oregon, USA.” Geomorphology 94 (1-2): 184–205.
https://doi.org/10.1016/j.geomorph.2007.05.009.
Minár, Jozef, Ian S. Evans, and Marián Jenčo. 2020.
“A Comprehensive System of Definitions of Land Surface (Topographic) Curvatures, with Implications for Their Application in Geoscience Modelling and Prediction.” Earth-Science Reviews 211 (December): 103414.
https://doi.org/10.1016/j.earscirev.2020.103414.
Montgomery, David R., and Efi Foufoula-Georgiou. 1993.
“Channel Network Source Representation Using Digital Elevation Models.” Water Resources Research 29 (12): 3925–34.
https://doi.org/10.1029/93wr02463.
Nüst, Daniel, and Edzer Pebesma. 2020.
“Practical Reproducibility in Geography and Geosciences.” Annals of the American Association of Geographers 111 (5): 1300–1310.
https://doi.org/10.1080/24694452.2020.1806028.
O’Callaghan, John F., and David M. Mark. 1984.
“The Extraction of Drainage Networks from Digital Elevation Data.” Computer Vision, Graphics, and Image Processing 28 (3): 323–44.
https://doi.org/10.1016/s0734-189x(84)80011-0.
Oregon Department of Forestry. 2022.
“Private Forest Accord Report.” Oregon Department of Forestry.
https://www.oregon.gov/odf/aboutodf/documents/2022-odf-private-forest-accord-report.pdf.
Patton, Nicholas R., Kathleen A. Lohse, Sarah E. Godsey, Benjamin T. Crosby, and Mark S. Seyfried. 2018.
“Predicting Soil Thickness on Soil Mantled Hillslopes.” Nature Communications 9 (1).
https://doi.org/10.1038/s41467-018-05743-y.
Reid, Mark E., Jeffrey A. Coe, and Dianne L. Brien. 2016.
“Forecasting Inundation from Debris Flows That Grow Volumetrically During Travel, with Application to the Oregon Coast Range, USA.” Geomorphology 273 (November): 396–411.
https://doi.org/10.1016/j.geomorph.2016.07.039.
Robison, G. E., K. A. Mills, J. Paul, L. Dent, and A. Skaugset. 1999. “Storm Impacts and Landslides of 1996: Final Report.” Oregon Department of Forestry.
Ruhe, Constantin. 2018.
“Quantifying Change Over Time: Interpreting Time-Varying Effects In Duration Analyses.” Political Analysis 26 (1): 90–111.
https://doi.org/10.1017/pan.2017.35.
Schilling, S. P. 1998. “LAHARZ: GIS Programs for Automated Mapping of Lahar-Inundation Hazard Zones.” Open File Report 98-638. US Geological Survey.
Shavers, Ethan, and Lawrence V. Stanislawski. 2020.
“Channel Cross-Section Analysis for Automated Stream Head Identification.” Environmental Modelling & Software 132 (October): 104809.
https://doi.org/10.1016/j.envsoft.2020.104809.
Shelef, Eitan, and George E. Hilley. 2013.
“Impact of Flow Routing on Catchment Area Calculations, Slope Estimates, and Numerical Simulations of Landscape Development.” Journal of Geophysical Research: Earth Surface 118 (4): 2105–23.
https://doi.org/10.1002/jgrf.20127.
Sîrbu, Flavius, Lucian Drăguț, Takashi Oguchi, Yuichi Hayakawa, and Mihai Micu. 2019.
“Scaling Land-Surface Variables for Landslide Detection.” Progress in Earth and Planetary Science 6 (1).
https://doi.org/10.1186/s40645-019-0290-1.
Soille, Pierre. 2004.
“Morphological Carving.” Pattern Recognition Letters 25 (5): 543–50.
https://doi.org/10.1016/j.patrec.2003.12.007.
Stock, J. D., and W. E. Dietrich. 2006.
“Erosion of Steepland Valleys by Debris Flows.” Geological Society of America Bulletin 118 (9-10): 1125–48.
https://doi.org/10.1130/b25902.1.
Tarboton, David G. 1997.
“A New Method for the Determination of Flow Directions and Upslope Areas in Grid Digital Elevation Models.” Water Resources Research 33 (2): 309–19.
https://doi.org/10.1029/96wr03137.
Tsunetaka, Haruka, Shiho Asano, and Wataru Murakami. 2022.
“Do Standing Trees Affect Landslide Mobility on Forested Hillslopes in Japan?” Earth Surface Processes and Landforms 47 (14): 3332–47.
https://doi.org/10.1002/esp.5461.
Wang, Yi-Jie, Cheng-Zhi Qin, and A-Xing Zhu. 2019.
“Review on Algorithms of Dealing with Depressions in Grid DEM.” Annals of GIS 25 (2): 83–97.
https://doi.org/10.1080/19475683.2019.1604571.
Wilson, John P., Graeme Aggett, Deng Yongxin, and Christine S. Lam. n.d.
“Water in the Landscape: A Review of Contemporary Flow Routing Algorithms.” In, 213–36. Springer Berlin Heidelberg.
https://doi.org/10.1007/978-3-540-77800-4_12.
Zevenbergen, Lyle W., and Colin R. Thorne. 1987.
“Quantitative Analysis of Land Surface Topography.” Earth Surface Processes and Landforms 12 (1): 47–56.
https://doi.org/10.1002/esp.3290120107.
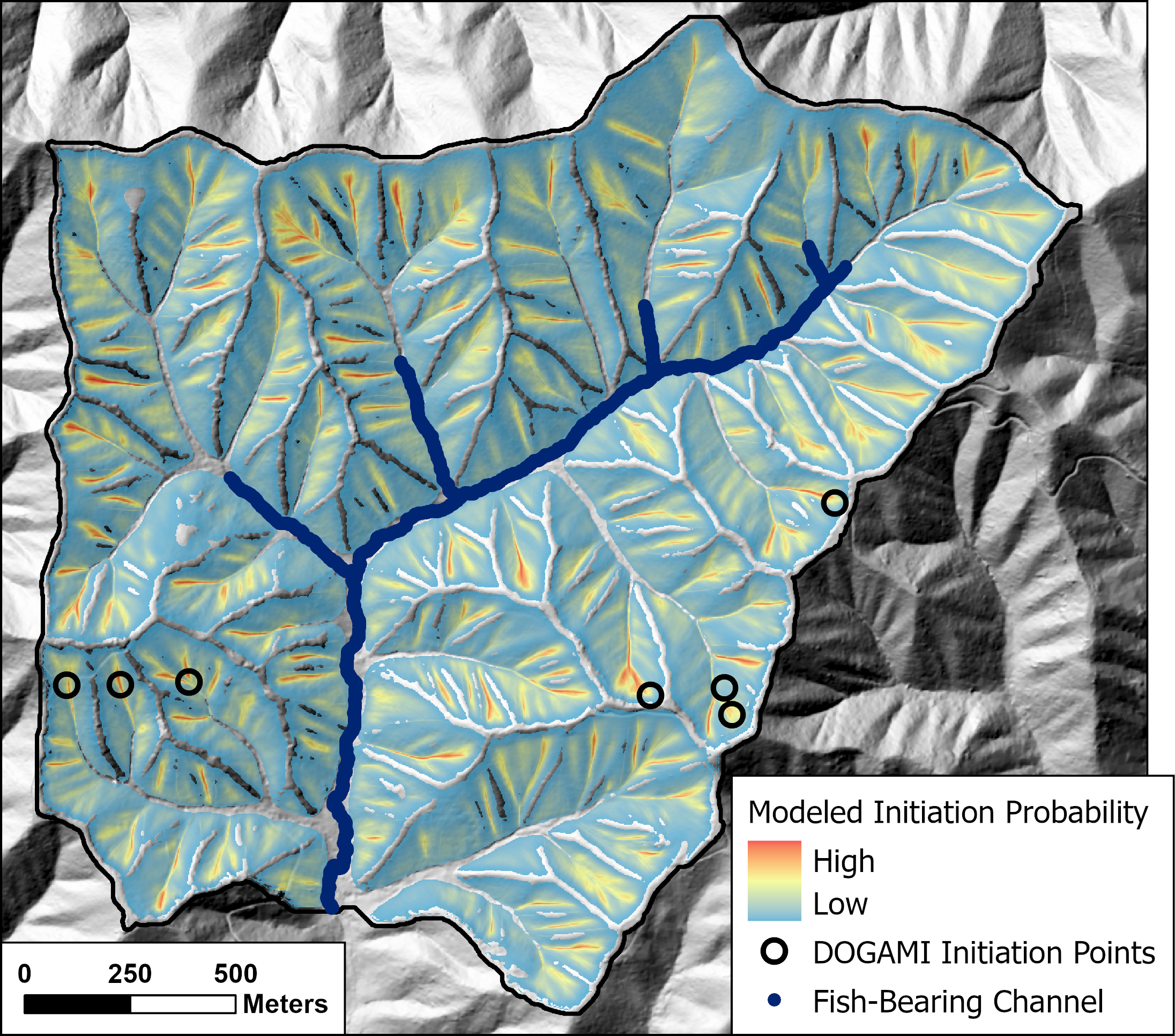
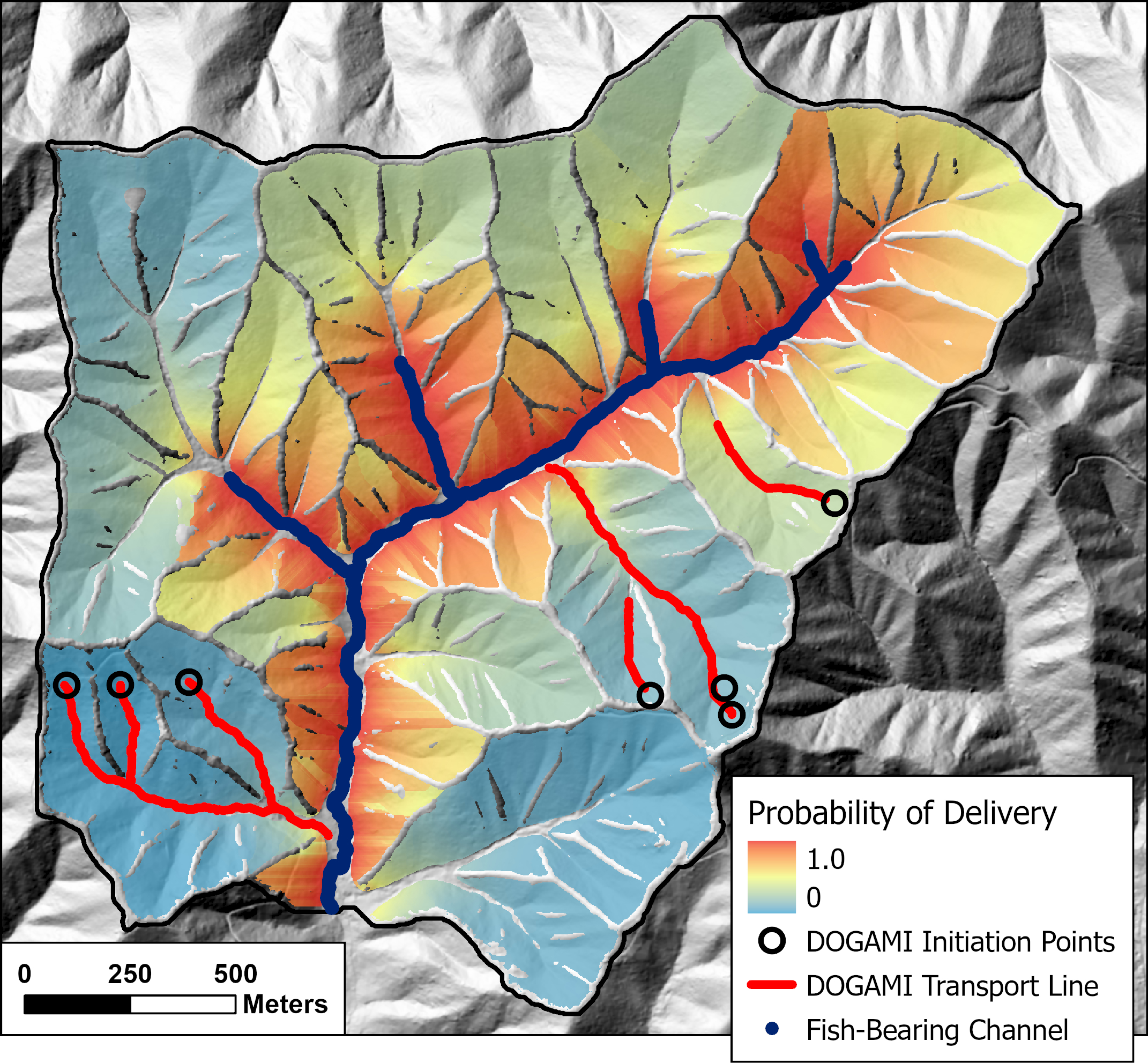
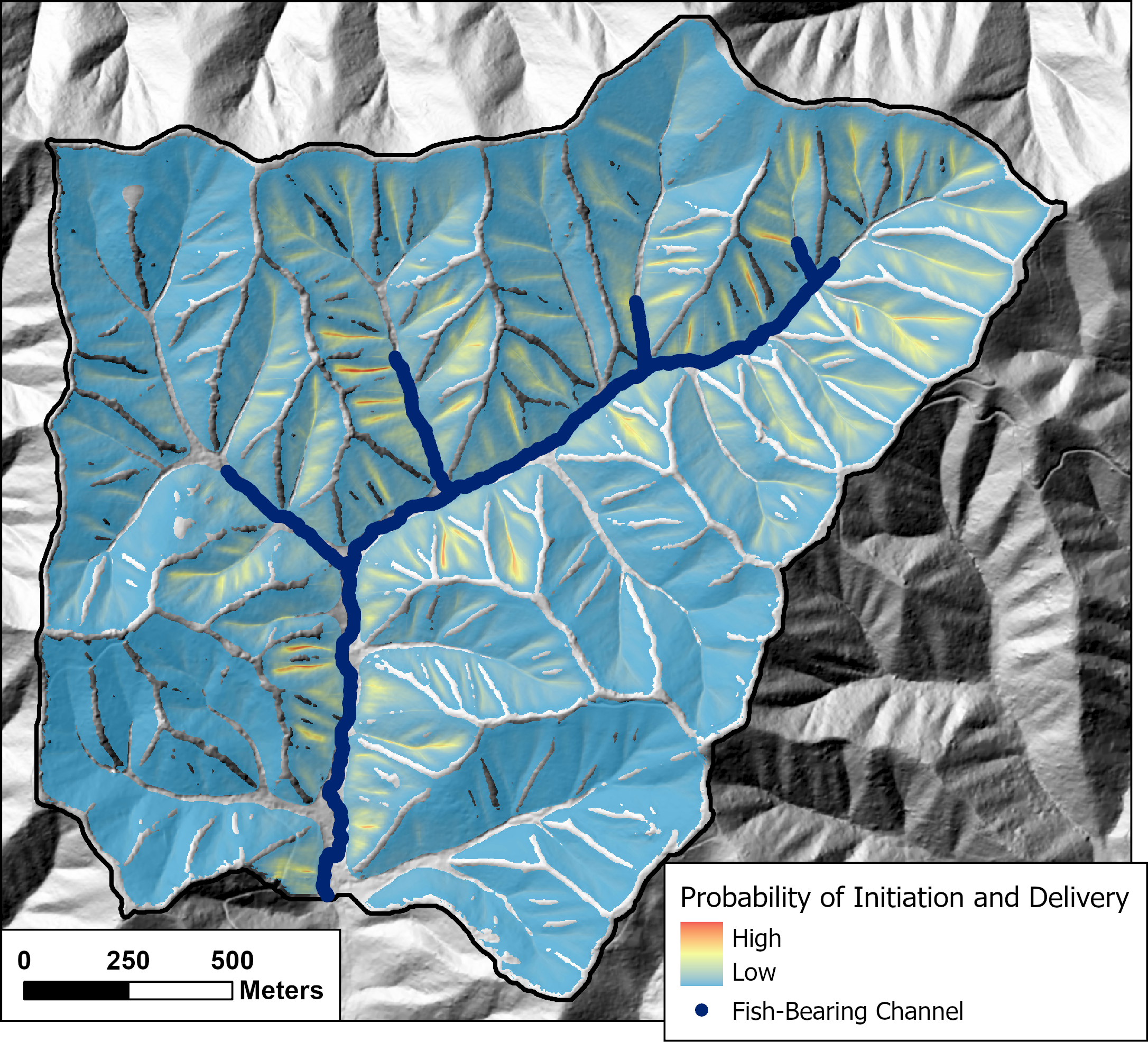

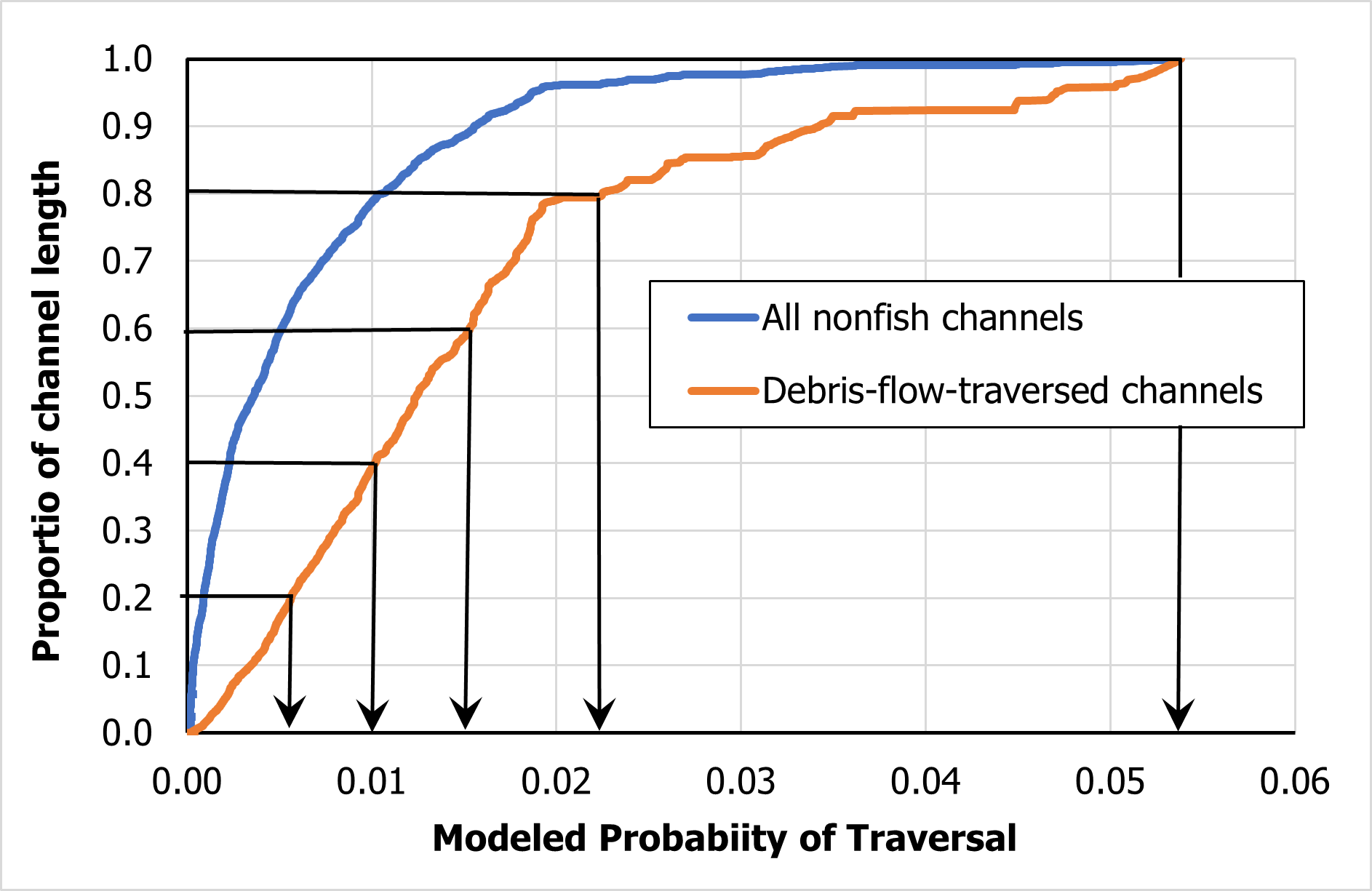
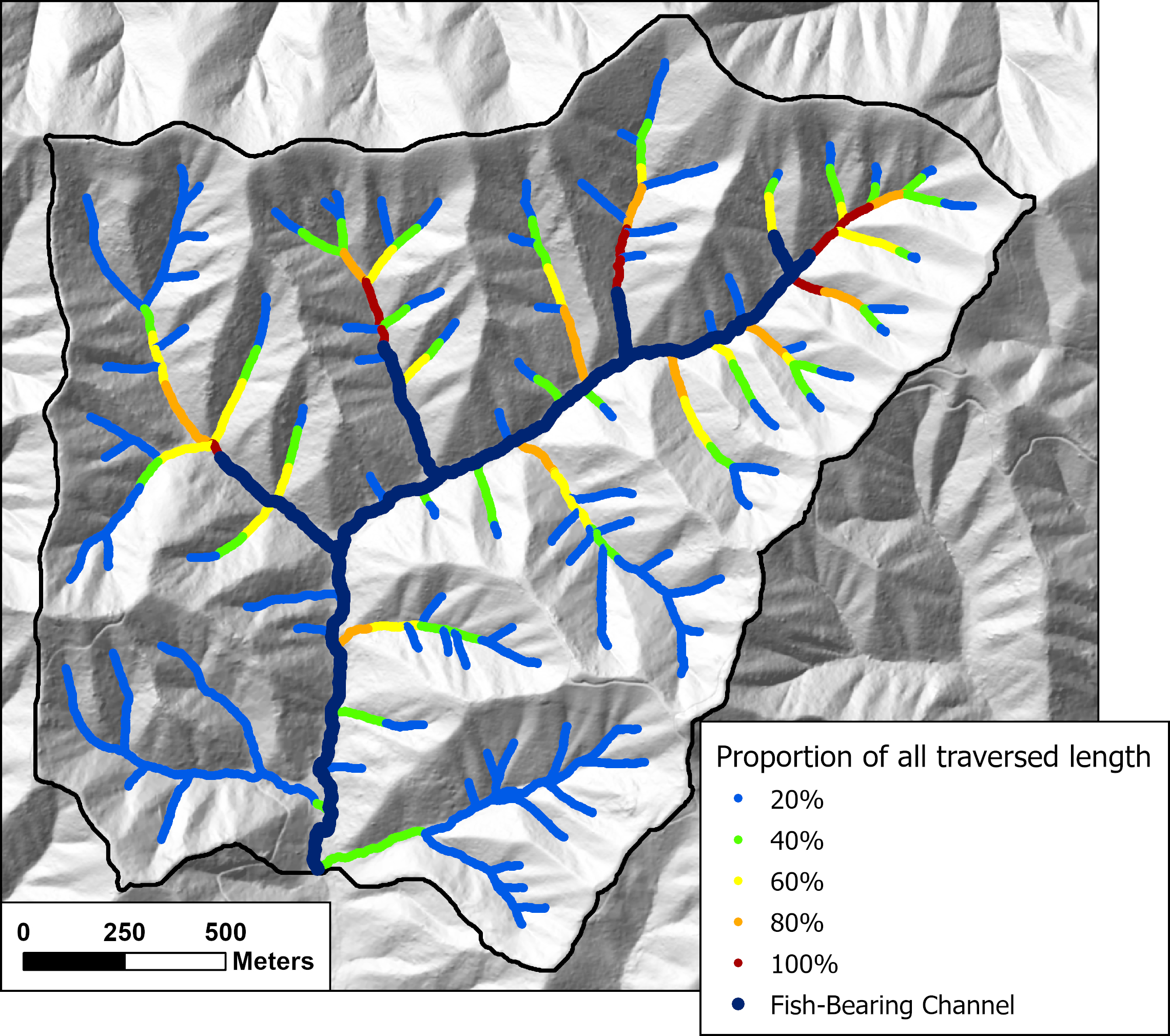
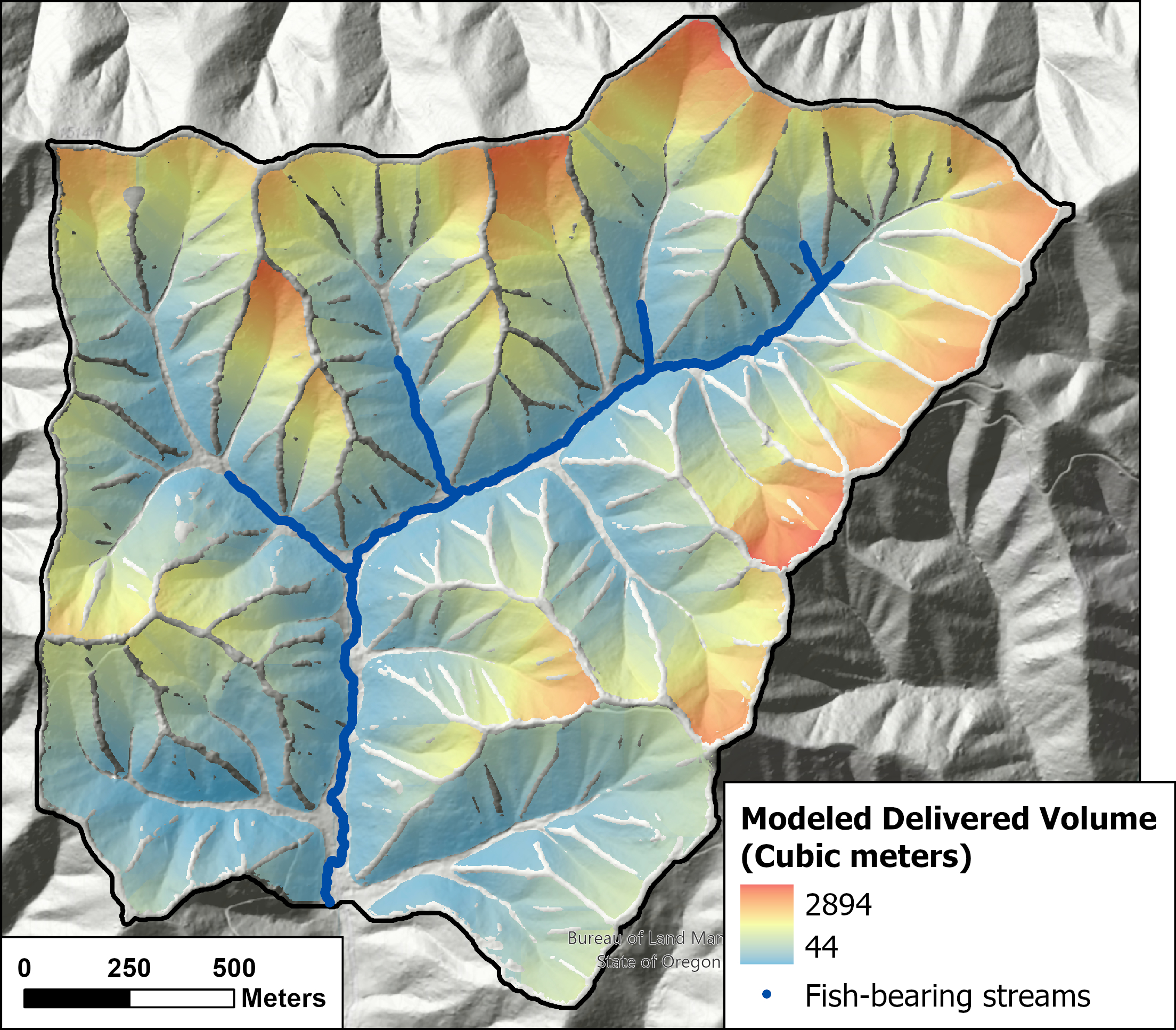
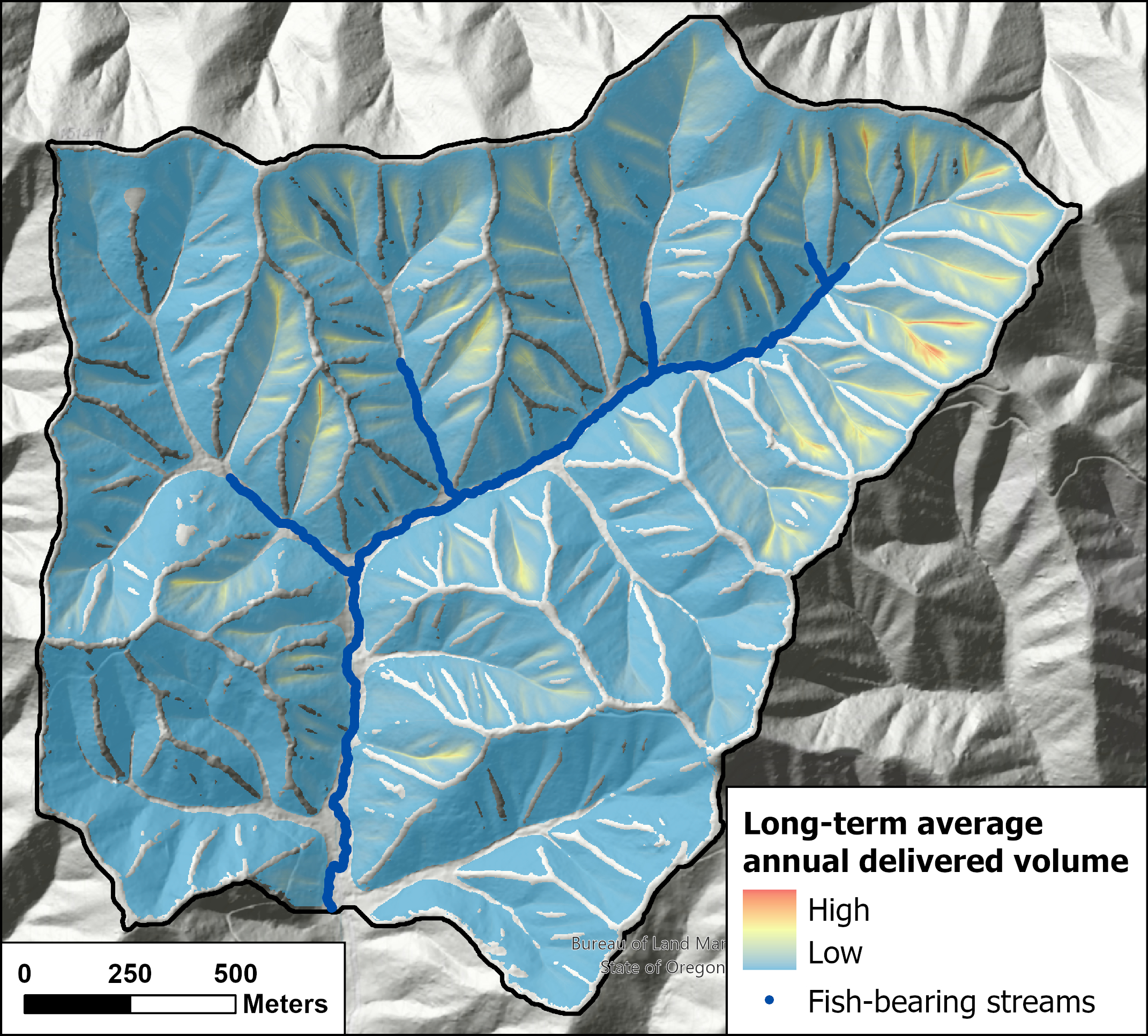
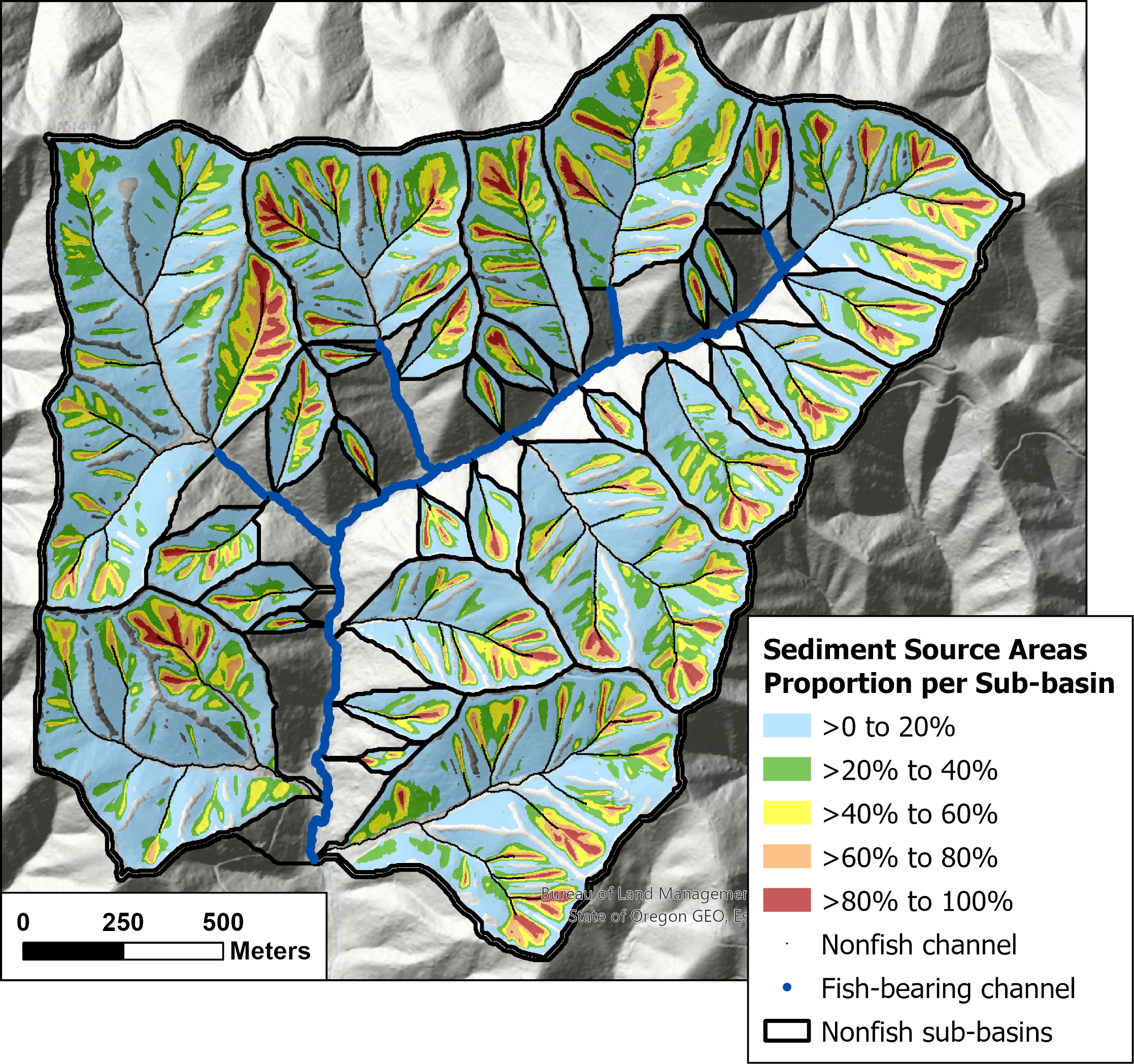
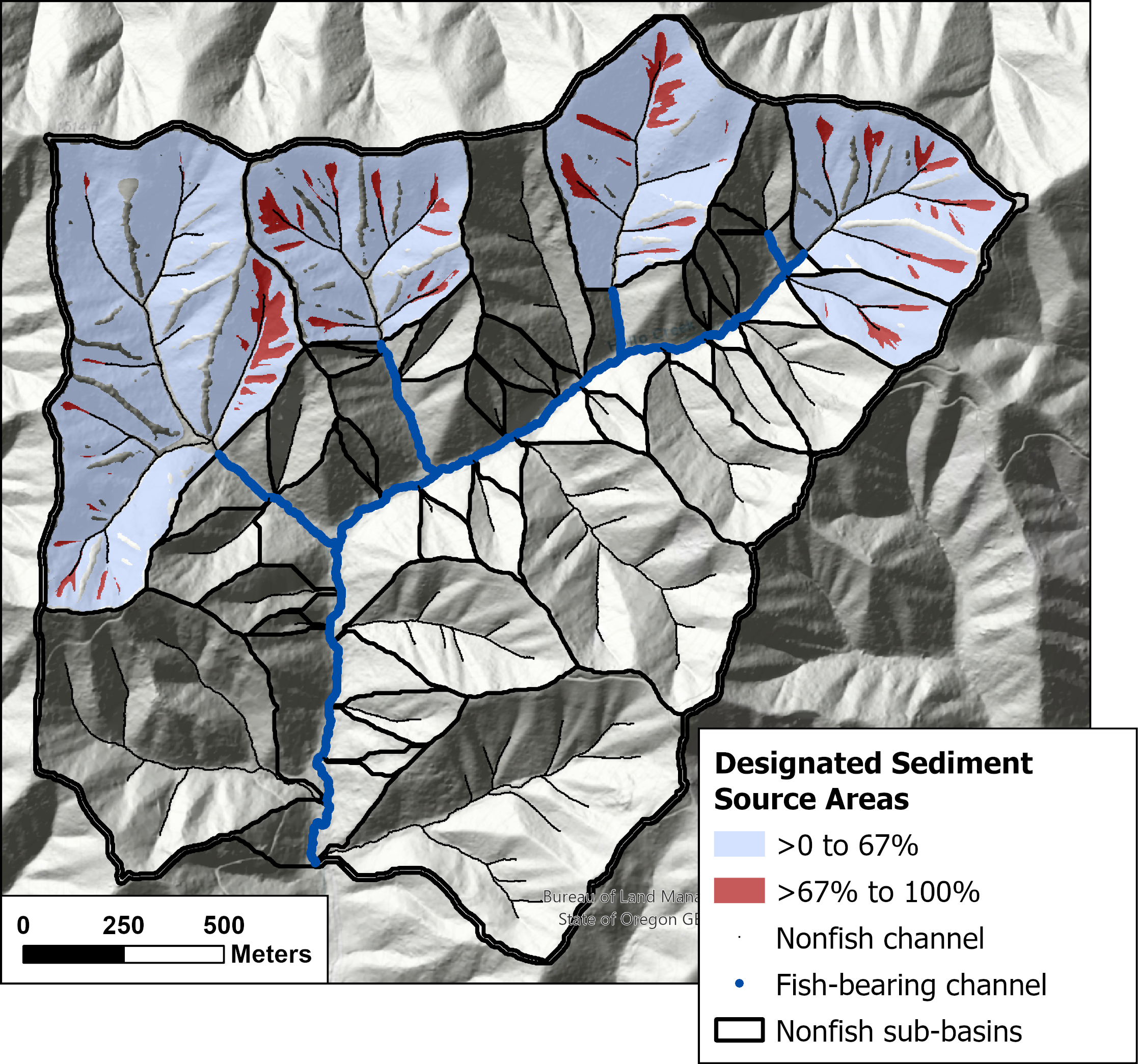
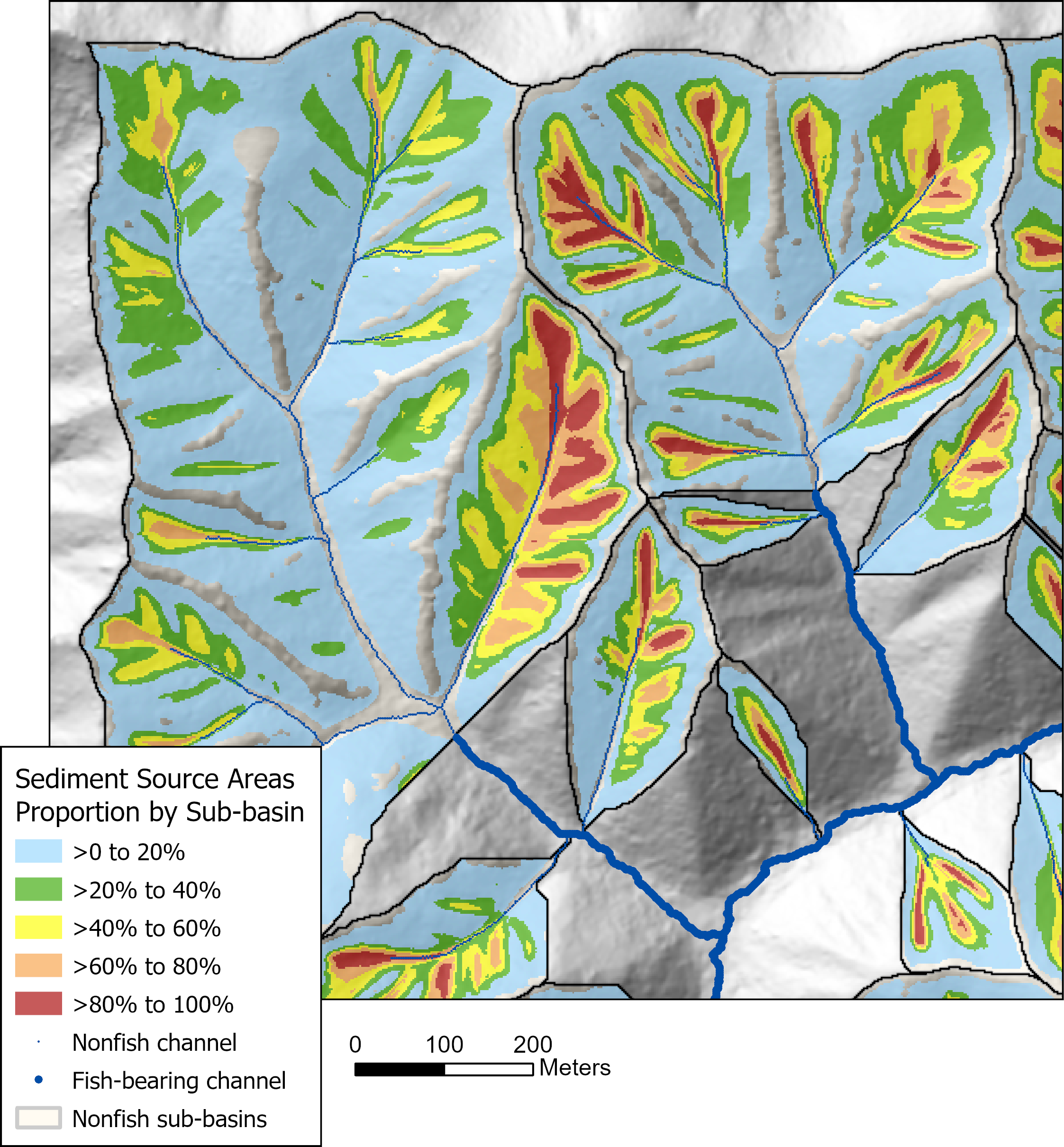


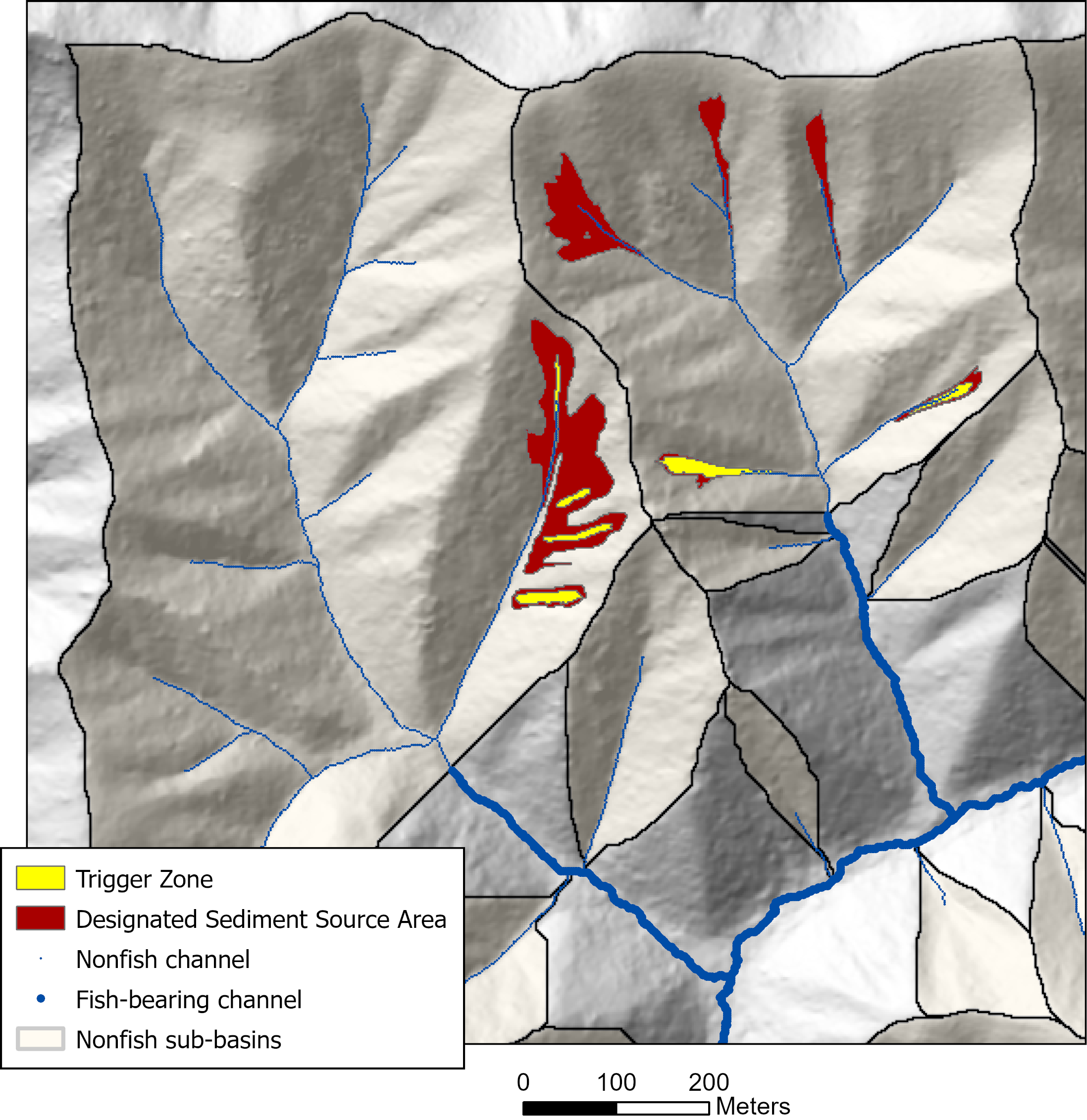

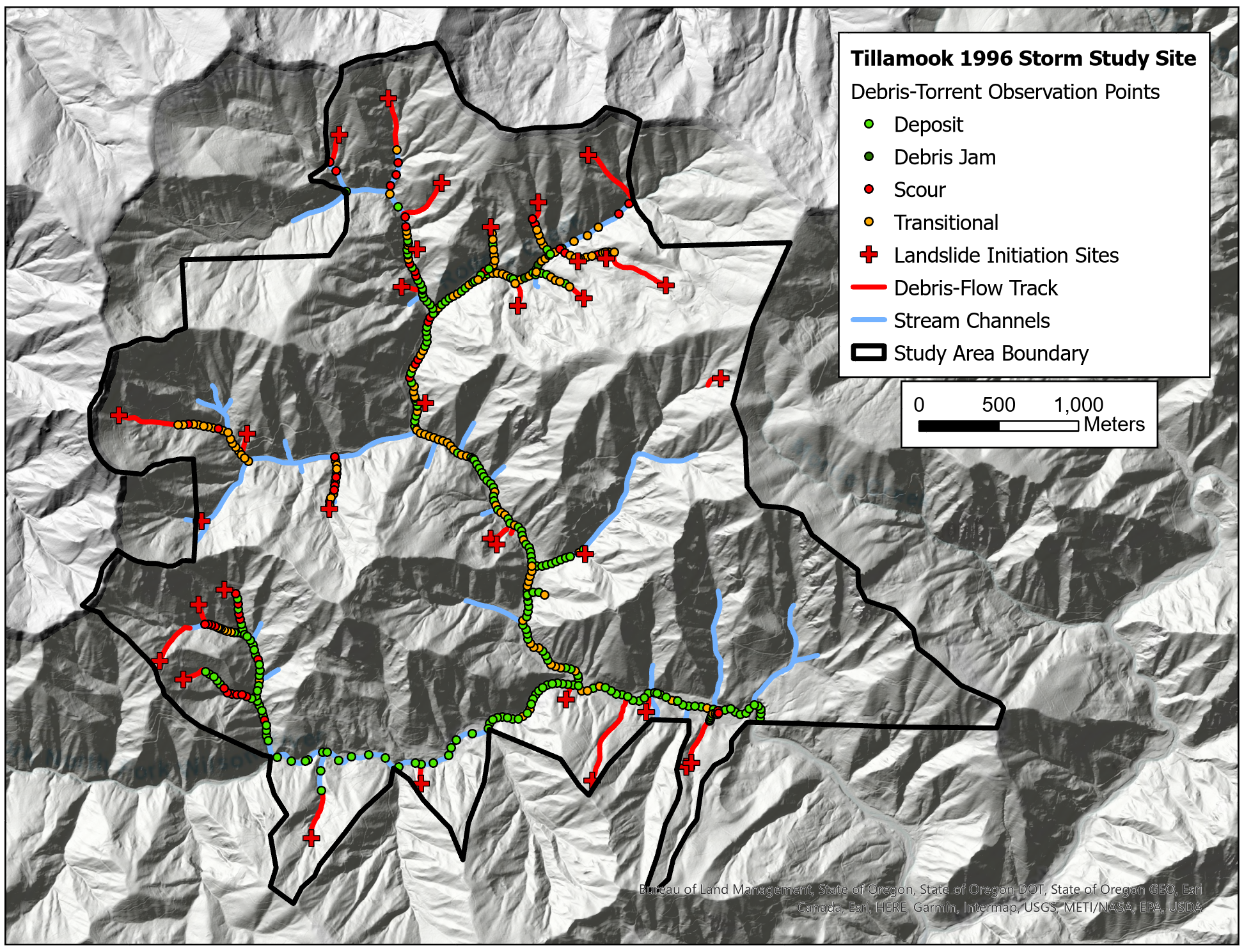

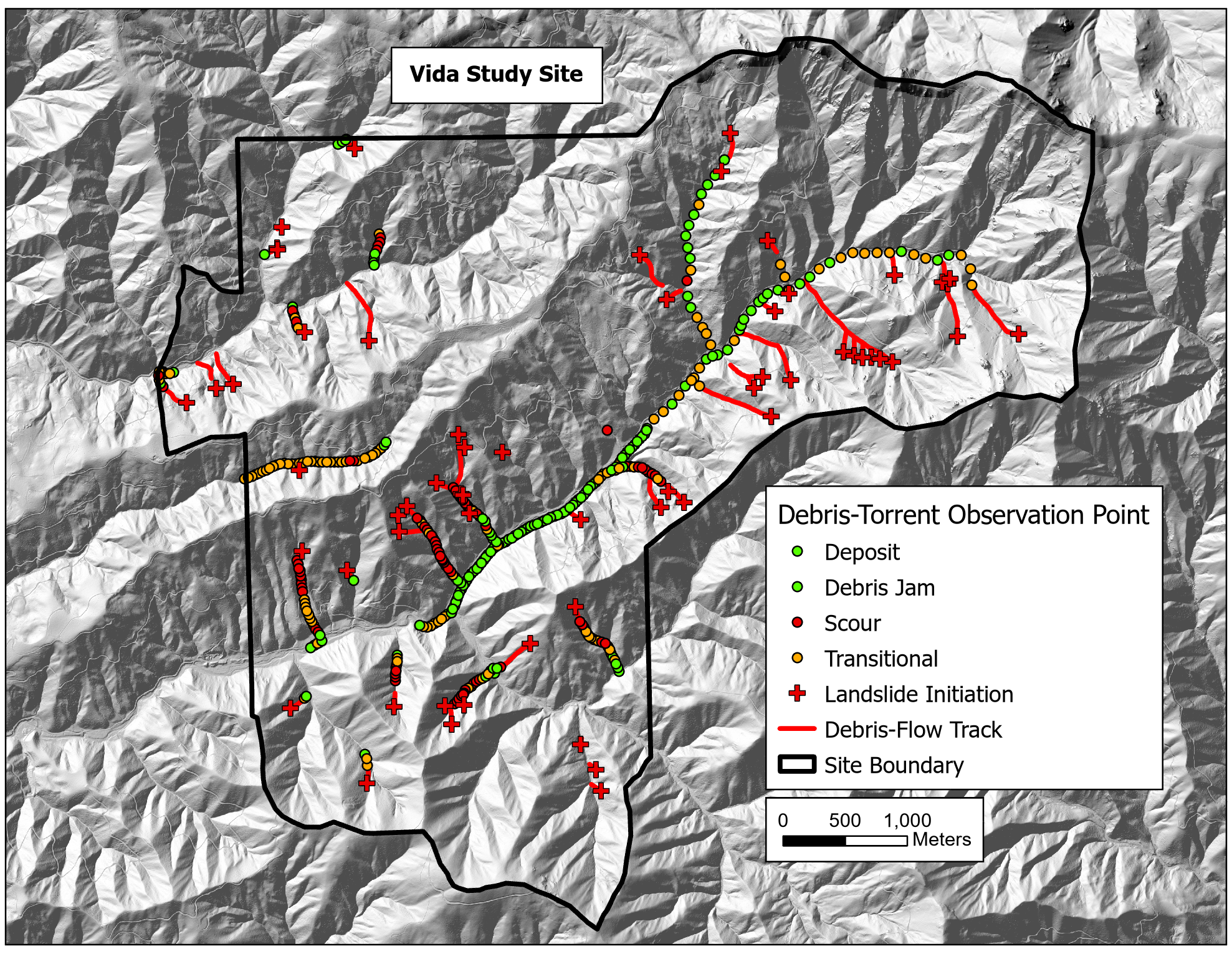
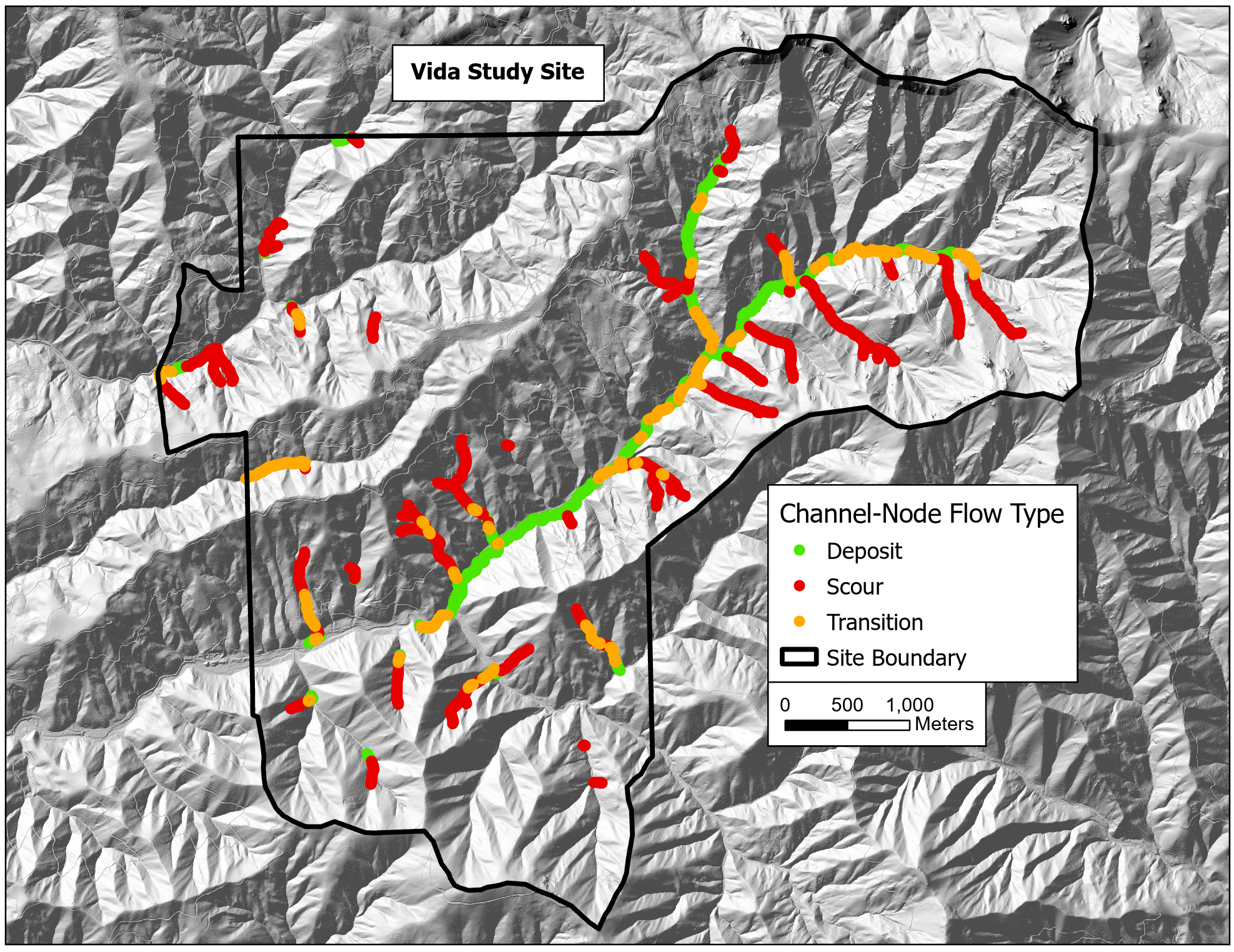
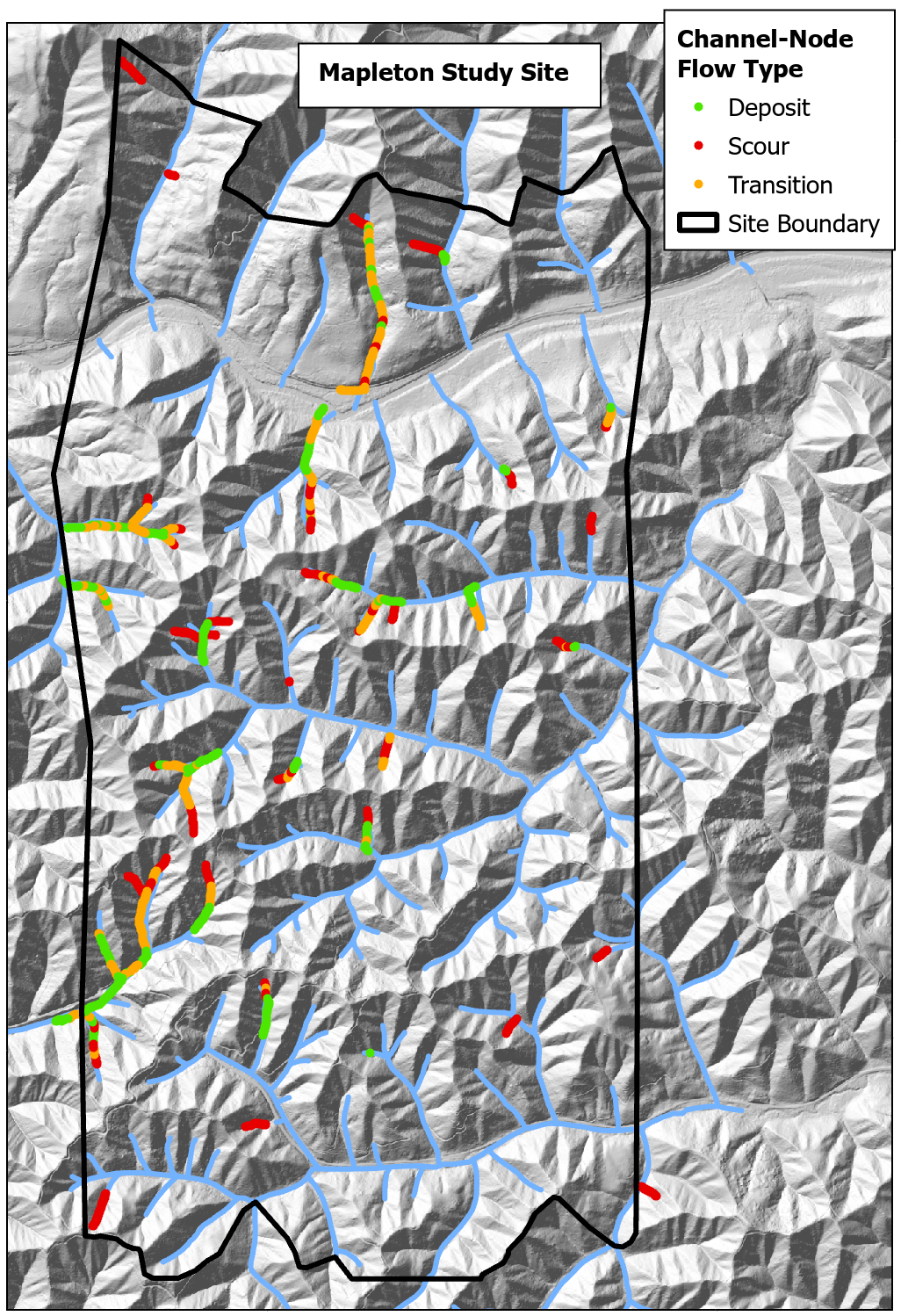 {fig-MapletonNodes}
{fig-MapletonNodes}